Solving the N-Queen Problem with C. The N-Queen Problem is a classic algorithmic challenge that involves placing N queens on an N*N chessboard so that no two queens can threaten each other. This means two queens can be in the same row, column, or diagonal. This article provides a step-by-step guide to solving the n queen problem with C language, focusing on a backtracking approach, which is a form of recursive algorithm.
Table of Contents
Understanding the N Queen Problem
Before jumping into coding, it is crucial to thoroughly understand what the n queen problem is and what it entails. the goal is to find all the problem arrangments of n queen on an n*n chessboard where no two queens attack each other.
Solving N Queen Problem with C
Defining the Chessboard
The chessboard can be represented as a 2D array of integers, where 0 indicates a space and 1 represents a queen.
int board[n][n];Initializing the Chessboard
Before starting ensure that the chessboard is empty. this can be done with the simple nested loop
void initalizeBoard(int board[n][n])
{
for (int i = 0; i < n; i++)
{
for (int j = 0; j < n; j++)
{
board[i][j] = 0;
}
}
}Check if the Queen can be Placed
We need a function to check if a queen can be placed on the board at the [row][col] position without being attacked by another queen.
int isSafe(int board[n][n], int row, int column)
{
int i, j;
// Check this row on left side
for (i = 0; i < column; i++)
{
if (board[row][i])
{
return 0;
}
}
// Check upper diagonal on upper side
for (i = row, j = column; i >= 0 && j >= 0; i--, j--)
{
if (board[i][j])
{
return 0;
}
}
// Check lower diagonal on left side
for (i = row, j = column; j >= 0 && i < n; i++, j--)
{
if (board[i][j])
{
return 0;
}
}
return 1;
}Solve the N Queen Problem
Use backtracking to solve the problem recursively. the function tries to place a queen on every row. if placing a queen in a certain column leads to the solution, it proceeds to place another queen in the next row. If it does not lead to a solution, it backtracks and tries a different column.
int solvenqueen(int board[n][n], int column)
{
// Base case: If all queens are placed
if (column >= n)
{
return 1;
}
// Consider this column and try placing this queen in all rows one by one
for (int i = 0; i < n; i++)
{
// Chcek if queen can be placed on board[i][column]
if (isSafe(board, i, column))
{
// Place this queen on board[i][column]
board[i][column] = 1;
// Recur to place rest of the queens
if (solvenqueen(board, column + 1))
{
return 1;
}
// If placing queens in board[i][column] does not need to a solution,
board[i][column] = 0;
}
}
// if the queen can't be placed in any row in this column then return false
return 0;
}Implement the Main Function
This function initializes the board and calls the utility function to solve the problem.
void main()
{
printf("Enter the value of n ");
scanf("%d", &n);
int board[n][n];
initalizeBoard(board);
if (!solvenqueen(board, 0))
{
printf("Solution does not exist");
}
else
{
printSolution(board);
}
}Print the Solution
Implement a function to print the chessboard with a Queen place.
void printSolution(int board[n][n])
{
printf("\n\n");
for (int i = 0; i < n; i++)
{
for (int j = 0; j < n; j++)
{
printf(" %d ", board[i][j]);
}
printf("\n");
}
printf("\n\n");
}Compelet C Program for N Queen Problem
#include <stdio.h>
#include <stdlib.h>
int n;
void printSolution(int board[n][n])
{
printf("\n\n");
for (int i = 0; i < n; i++)
{
for (int j = 0; j < n; j++)
{
printf(" %d ", board[i][j]);
}
printf("\n");
}
printf("\n\n");
}
int isSafe(int board[n][n], int row, int column)
{
int i, j;
// Check this row on left side
for (i = 0; i < column; i++)
{
if (board[row][i])
{
return 0;
}
}
// Check upper diagonal on upper side
for (i = row, j = column; i >= 0 && j >= 0; i--, j--)
{
if (board[i][j])
{
return 0;
}
}
// Check lower diagonal on left side
for (i = row, j = column; j >= 0 && i < n; i++, j--)
{
if (board[i][j])
{
return 0;
}
}
return 1;
}
int solvenqueen(int board[n][n], int column)
{
// Base case: If all queens are placed
if (column >= n)
{
return 1;
}
// Consider this column and try placing this queen in all rows one by one
for (int i = 0; i < n; i++)
{
// Chcek if queen can be placed on board[i][column]
if (isSafe(board, i, column))
{
// Place this queen on board[i][column]
board[i][column] = 1;
// Recur to place rest of the queens
if (solvenqueen(board, column + 1))
{
return 1;
}
// If placing queens in board[i][column] does not need to a solution,
board[i][column] = 0;
}
}
// if the queen can't be placed in any row in this column then return false
return 0;
}
void initalizeBoard(int board[n][n])
{
for (int i = 0; i < n; i++)
{
for (int j = 0; j < n; j++)
{
board[i][j] = 0;
}
}
}
void main()
{
printf("Enter the value of n ");
scanf("%d", &n);
int board[n][n];
initalizeBoard(board);
if (!solvenqueen(board, 0))
{
printf("Solution does not exist");
}
else
{
printSolution(board);
}
}Output of N Queen Solution
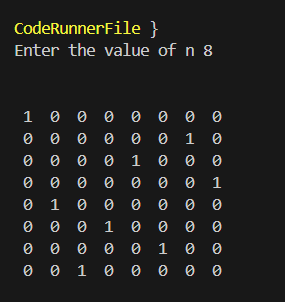
n = 8
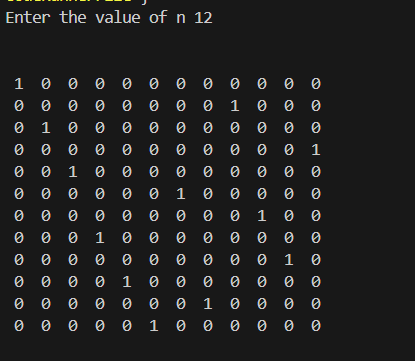
n=12
N Queen Problem Time Complexity
The backtracking approach for solving the n queen problem, as demonstrated in this article by using C language, does not have a straightforward time complexity due to its recursive nature and the fact that it explores multiple branches of execution, backtracking when a potential solution does not lead to success. The worst-case time complexity for the n queen problem using backtracking can be roughly estimated as O(n!) where n is the number of queens(or the size of the chessboard). This factorail time complexity arises because, in the worst case, the algorithm might need to try all possible arrangements of n queens on the board.
Happy Coding & Learning
2 thoughts on “Solving the N Queen Problem with C”