1 2 3 4 Series Program in C

by

In the world of programming & coding, the creation and manipulation of sequences play a fundamental role in algorithmic understanding. The 1 2 3 4 series is a sequence pattern that involves generating numbers in a specific order: 1, 2, 3, 4, 5, 6 and so forth. This pattern is a fascinating concept and holds significance in various programming applications.

Concept of the 1 2 3 4 Series

The series 1, 2, 3, 4,… represents a sequence of natural numbers starting from 1 and incrementing by 1 continuously. This progression forms the core logic of our program.

1 2 3 4 Series Implementation in C

Let’s write a simple C program to generate the 1 2 3 4 series:

#include <stdio.h>

void main() {
  int n, i;
  printf("Enter the maximum number: ");
  scanf("%d", &n);

  for (i = 1; i <= n; i++) {
    printf("%d ", i);
  }
}

Output

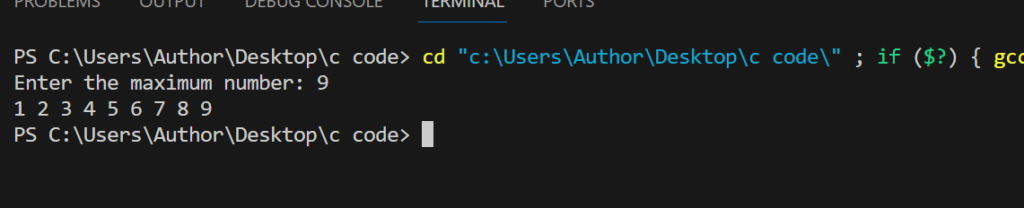
1 2 3 4 Series Program in C

How the Above C Program Works for 1234 Series

  • We declare a variable (i) to represent the current number in the series.
  • We initialize i to 1 (the starting number).
  • We set a loop condition based on the desired ending point (say, n).
  • Inside the loop body, we print the current value of i.
  • After printing, we increment i by 1 to move to the next number in the series.
  • The loop iterates until the stopping condition is met, resulting in the desired sequence.

This program serves as a foundation for exploring more complex concepts. We can modify it to –

  • Print the series in reverse order.
  • Calculate and print the sum of the series.
  • Generate different sequences with varying increments or starting points.

See Also

Leave a Comment