Shell Sort in Java

Shell Sort in Java. Shell sort, a highly efficient algorithm, offers a distinct approach to arranging elements in an array by diminishing the number of swaps required to sort the entire list. Shell sort algorithm, introduced by Donald Shell in 1959, Extends the concept of insertion sort by allowing the comparison and exchange of elements that are far apart, rather than adjacent. This method significantly reduces the total number of moves required, making shell sort particularly effective for moderately sized arrays. In this article, we will explore the implementation of shell sort in Java, its algorithmic logic, and its performance characteristics.

Understanding Shell Sort

Shell sort improves upon the insertion sort algorithm by initially sorting elements far apart from each other and gradually reducing the gap between elements to be compared. This technique is known as the “Diminishing” increment sort. By partially sorting the array with wider gaps, The shell sort algorithm ensures that when the gap is reduced, the array is already more sorted than at the beginning. The final stage of the algorithm is a simple insertion sort but by this time, the array is already nearly sorted, which is an ideal scenario for insertion sort.

Shell Sort Algorithm Steps

Initialization: Start with the large gap, often set as half the length of the array.
Gap Reduction: After each pass, reduce the gap. A common method is to half the gap each time until it becomes 0.
Sorting: For each gap, perform a gapped insertion sort. This means elements in the array are compared and swapped if necessary, not just with their immediate neighbors but with elements a gap distance away.

Here is a simple Java implementation of the Shell sort algorithm.

package CodingProblems;

public class ShellSort {
public static void shellsort(int array[], int n)
    {
        for (int gap = n / 2; gap > 0; gap /= 2) {
            for (int i = gap; i < n; i += 1) {
                int temp = array[i];
                int j;
                for (j = i; j >= gap && array[j - gap] > temp; j -= gap) {
                    array[j] = array[j - gap];
                }
                array[j] = temp;
            }
        }
    }

    public static void main(String[] args) {
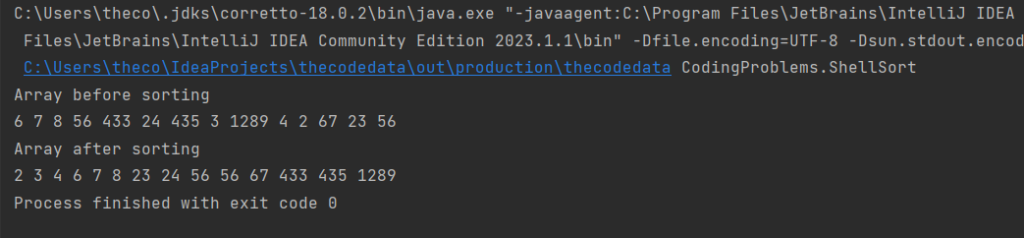
        int array[] = {6, 7, 8,56,433,24,435,3, 1289, 4, 2, 67, 23, 56};
        int n = array.length;
        System.out.println("Array before sorting");
        for (int i = 0; i < n; i++)
        {
            System.out.print(array[i]+" ");
        }
        shellsort(array, n);
        System.out.println("\nArray after sorting");
        for (int i = 0; i < n; i++)
        {
            System.out.print(array[i]+" ");
        }
    }
}

Output

Performance Analysis of Shell Sort

Shell sort’s time complexity varies based on the gap sequence used. The worst case and complexity are known to be in the range of O(n^2), depending on the gap sequence, but the best gap sequence and reduced time complexity of shell sort to O(n^1.5).

However, unlike more complex algorithms like quick sort or merge sort, Shell sort does not require additional memory for its operation, making it a space efficient, in-place sorting algorithm.

Happy Coding & Learning

Shell Sort in Java

Table of Contents

Understanding Shell Sort

Shell Sort Algorithm Steps