Matrix Transpose in Java. Matrix operations are crucial in various computational domains, including data analytics, scientific computing, and image processing. One fundamental operation in matrix manipulation is a transposition, which reorients a matrix of rows and columns. This article will explore matrix transposition and demonstrate how to implement this operation in Java.
Table of Contents
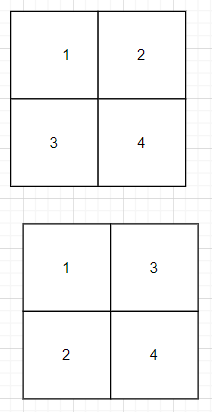
Background of Matrix Transposition
Matrix Transposition is a formative operation in linear algebra where columns and rows of a matrix are interchanged, producing a new matrix. Mathematically if we denote a matrix by A, it transposes is represented by A^T. The elements at row i and column j in the original matrix become the elements at row j and column i in the transpose matrix.
Implementing Matrix Transposition in Java
Java, being the robust, object-oriented programming language, offers a structured approach to implementing matrix transposition. Below, we delve into a more comprehensive Java implementation that covers dynamic matrix generation and transposition.
Dynamic Matrix Creation
In Java, matrices can be represented using two-dimensional arrays unlike C, Java supports dynamic array allocation, Allowing for flexible Matrix sizes.
Scanner sc = new Scanner(System.in);
System.out.println("Enter the number of rows");
int rows = sc.nextInt();
System.out.println("Enter number of columns ");
int columns = sc.nextInt();
int [][] matrix = new int[rows][columns];Matrix Input in Java
Next, We populate the matrix with values entered by the user, utilizing a nested loop, here we use two nested for loops.
System.out.println("Enter the matrix elemnts");
for(int i=0;i<rows;i++) {
for(int j=0;j<columns;j++) {
matrix[i][j] = sc.nextInt();
}
}Transpose Operation in Java
We transpose the matrix by swapping the rows and columns. In Java, this involves creating a new matrix where the dimensions are invented (where i=j, j=1). For this operation also we need a nested for loop.
int [][] transpose = new int[columns][rows];
for(int i=0;i<rows;i++) {
for(int j=0;j<columns;j++) {
transpose[j][i] = matrix[i][j];
}
}Displaying the Transpose Matrix
Now finally we will print the resultant transposed matrix.
System.out.println("Transposed Matrix");
for(int i=0;i<columns;i++) {
for(int j=0;j<rows;j++) {
System.out.print(transpose[i][j]+" ");
}
System.out.println();
}Complete Java Program for Matrix Transpose
import java.util.Scanner;
public class MatTransposition {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
System.out.println("Enter the number of rows");
int rows = sc.nextInt();
System.out.println("Enter number of columns ");
int columns = sc.nextInt();
int [][] matrix = new int[rows][columns];
System.out.println("Enter the matrix elemnts");
for(int i=0;i<rows;i++) {
for(int j=0;j<columns;j++) {
matrix[i][j] = sc.nextInt();
}
}
int [][] transpose = new int[columns][rows];
for(int i=0;i<rows;i++) {
for(int j=0;j<columns;j++) {
transpose[j][i] = matrix[i][j];
}
}
System.out.println("Transposed Matrix");
for(int i=0;i<columns;i++) {
for(int j=0;j<rows;j++) {
System.out.print(transpose[i][j]+" ");
}
System.out.println();
}
}}
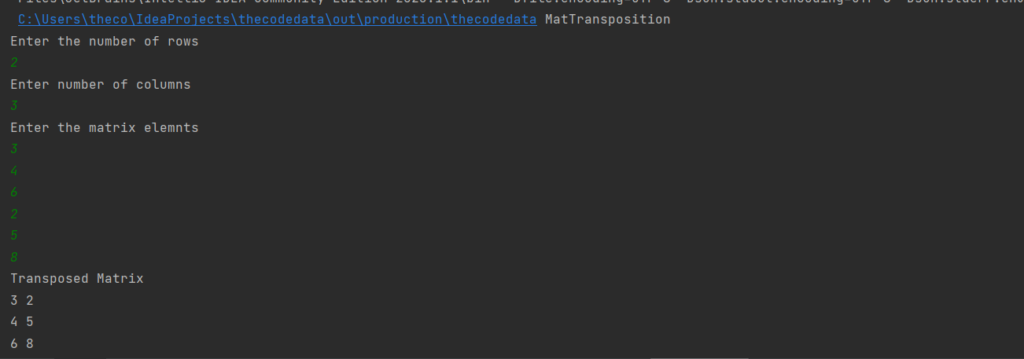
Output
Extending Functionality and Optimization
When implementing matrix transposition in Java there is a lot more to consider beyond the basic swapping of elements between rows and columns. Advanced programming techniques and optimization can enhance the efficiency and functionality of your matrix transposition code. Let’s see how we can see the functionality and optimize our Java implementation for better performance.
Extending Functionality for Better Performance
One of the main advantages of Java is its object-oriented nature, which allows for modular and reusable code. By encapsulating the matrix operation within a Java class, we can extend functionality in numerous ways:
Encapsulation and Abstraction
We can create a matrix class that encapsulates the matrix data and operations. This class can store the matrix data and provide methods for, transposing, adding, multiplying, subtracting matrices, and more. Abstraction hides the complex underlying operations from the user, making the code more readable and maintainable.
Generics and Flexibility
Using Java Generics we can create a more flexible matrix class that can handle different types of data, not just integers. This is particularly useful in scientific computing where matrices might contain complex numbers, floating points,s or other data types.
Optimization
Matrix operations can be computationally intensive, specially with large matrices. Optimization is the key to improving performance.
Loop Unrolling and Block Transposition
One way to optimize matrix transposition is by using loop unrolling and block transposition techniques. Loop unrolling reduces the overhead of the loop control structure, while lock transposition minimizes cache misses by transposing a small sub-matrix at a time.
Parallel Processing
Java concurrency utilities can be leveraged to perform matrix operations in parallel. This is especially effective for large matrices where operations like transposition can be divided into smaller tasks and executed concurrently.
Memory Management
Efficient memory management is crucial. Java’s garbage collector can handle deallocation but being mindful of memory allocation during matrix operation can reduce overhead. For instance, reusing existing matrices instead of creating new ones for every operation can significantly reduce memory use.
Matrix transposition is more than a textbook example; It is a critical operation used in a plethora of applications ranging from engineering to artificial intelligence. By understanding and applying advanced Java programming techniques, such as encapsulation, generic, and concurrency, programmers can enhance the performance and functionality of matrix operation.
As we have seen, expanding functionality and optimizing matrix transposition can lead to significant improvement in performance and useability. Whether in academic research, Industry application, or software development, the skills to effectively manipulate matrices in Java are invaluable. with these advanced techniques, you can tackle complex problems more efficiently and pave the way for innovative solutions in computational tasks.
Happy Coding & Learning